どうすれば正しく動くかな?の答え
秒針の1周は360度 1分間は60秒 下のコードの数字を何度にすると、秒針が正しく動くかな?
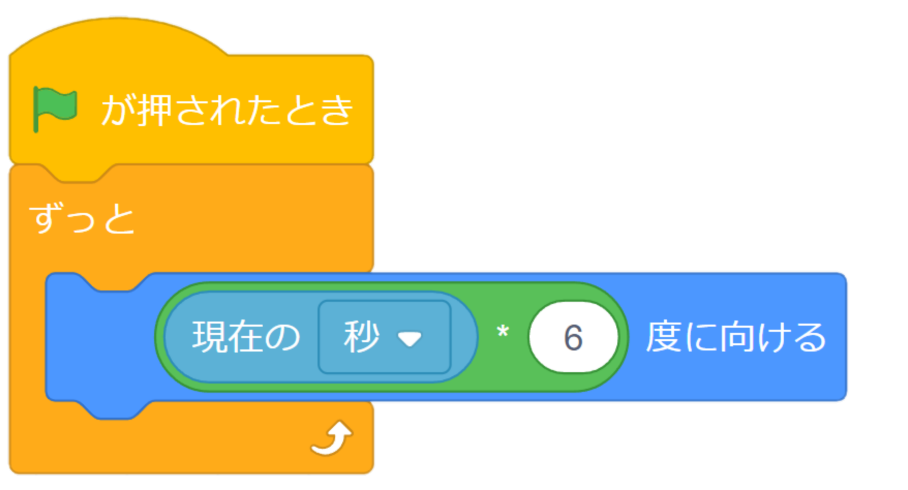
答えは「6」
秒針は60秒で1周します。つまり1分経過したという事ですね。
1周は360度なので、360÷60=6になります。
6度ずつを60回そういう風に秒針は動いています。
分針も同じような考え方で、60分で1周つまり1時間経過する事に
なるので、同じく1分間に6度ずつ動かします。
チャレンジ!の答え
時針は1分ごとに少しずつ動き 12時間かけて1周回ります。 時針はどうすれば正しく動くかな? ※現在の時も現在の分も使う事が出来ます。
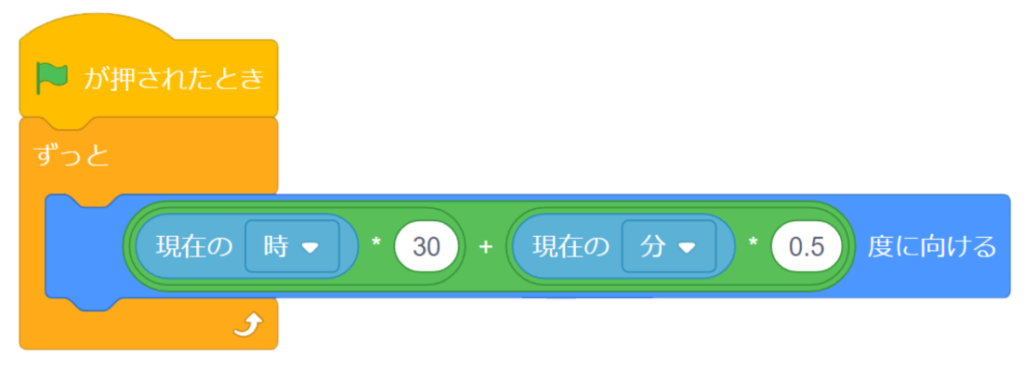
答えは「現在の(時)×30」+「現在の(分)×0.5」
なんだかちんぷんかんぷんですね。ひとつずつ解き明かしていきましょう。
まず、時針は12時間で1周回ります。
秒針の角度と同じ式にしてみます。360÷12=30
つまり1時間で30度進みます。なので現在の(時)×30は現在の時を表しています。これだけでも時計としては正解なんですが、これだと1時間に一回しか時針が動きません。30度も動くのですごく不自然です。
アナログ時計を見てみると、分針が動くにつれて少しずつ時針が動いていませんか?その答えがもう一つの式現在の(分)×0.5になります。
なぜ0.5なのか。それはさっきの時針の30度がカギになります。
時針は1時間で30度動く。分針は1時間60分。
分針を動かしながら時針が動かせそうな気がしませんか?
そうです。1分間に0.5度ずつ動かしてあげる事で、1時間に30度動くように
1時間未満の動きを表現する事が出来ます。
1時間経った時、変にならないかな?と思ったかもしれませんが、大丈夫。
分の始まりは0です。0はどの数字を掛けても0になります。
そして丁度分針が0分になった時、時針は次の数字になります。
そうする事でつじつまが合うようになります。
チャレンジは難しかったかもしれませんが、0をうまく使うのはプログラム開発ではとても重要な事です。
プログラムを開発する現場では、答えの無い事を工夫しながら近づける・探す作業がとても多くあります。
なので自分で考える力や面白さ・使いやすさなど伝える力などが必要です。
上記の答えは一例ですが、ただ問題を解くというより「少しずつ動かせるようにするにはどうすればいいのかな?」
という工夫を探す事の方がとても大切です。他にも出来たという方法があったら知らせてくださいね。
本教室では、テキスト的な模範解答に沿ったカリキュラムではなく、筋道を立てて解決出来る力をサポートしたいと考えています。